
Elasticity
The next progression of the projectile was the utilisation of elasticity in the form of bows and arrows. There is evidence of the use of the traditional bow and arrows dating back to almost 70,000 years ago in Africa. They were a very prevalent weapon in warfare throughout the the world up until the late middle ages and were the weapon of choice of the second largest empire of all time, the Mongol empire.
Information in these green boxes is considered advanced reading! Read this information if you want to learn more.
Types of Bow

TYPES OF BOW
There are two main types of bow. The first is the traditional bow which the archer must draw, aim and shoot in quick succession. Millenia after the traditional bow began being used however, the crossbow was invented. This was an advancement as it allowed the archer to ‘cock’ the crossbow, leaving it as long as needed, saving energy.
Mathematics of Flight

MATHEMATICS: FLIGHT
The mathematics of the flight of an arrow fired from a bow are easily described by the SUVAT equations, for which the terms are defined here
To work out the range of an arrow, we need to know the horizontal and vertical components of its initial velocity. If the arrow is fired at an angle to the horizontal at an initial speed u, the horizontal and vertical velocities can be worked out by resolving the resultant speed at a given point, as demonstrated in the figure below, with the general velocity term v. There is a constant vertical acceleration which is represented by the acceleration due to gravity; g.
To find the time t at which the arrow hits the floor we must set the vertical displacement equal to zero. Now that we have the displacement, acceleration, and initial velocity in the vertical plane, we can calculate the time the arrow has been in flight for using the second SUVAT equation . This is a quadratic equation which will give us two values for t. Under the assumption that the plane is perfectly flat, one solution will be negative. The other solution is our time at which the arrow hits the ground after being fired, and this is given by the positive solution to the quadratic in t. This equation is found to be;
This equation is particularly useful in also helping us prove that the maximum horizontal range of an arrow is generated by an angle of 45° (also proved here). To show this, we simply differentiate this last equation with respect to θ and set it to zero. This now gives us an equation in which our value for theta is optimised for the range of the arrow. This is given by the following equation:
It is now a simple matter of rearranging for theta to find:
Now that we know when our arrow hits the ground we can find out its range by using the same equation in the horizontal plane. Our value for acceleration is now zero, as we are operating under the assumption that there is no air resistance.
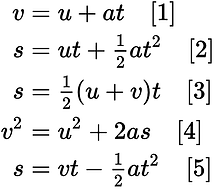
This is known as parabolic motion and is a much-simplified model for the flight of an arrow due to the assumptions it makes. Flaws in the model include that it does not account for air resistance. While the fletchings, head and shaft of an arrow are streamlined to make it as aerodynamic as possible, there will inevitable be some resistive force in the form of drag. This manifests itself as a deceleration in the direction of motion of the arrow and is caused by collisions between air particles and the arrow. This would cause our range to be an overestimation and it is likely that the bowmen would adjust their firing angle and power accordingly.
Our mathematics is also simplified as we are operating under the assumption of zero intial vertical displacement. This can be accounted for in our calculations by having an initial displacement S0. We still obtain a quadratic equation with real solutions, and can therefore still calculate the range of our arrow on planes which are not flat.
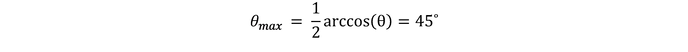

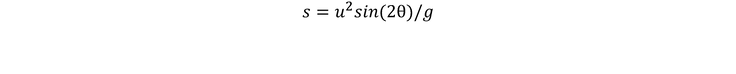

MATHEMATICS: ELASTICITY
The mathematics of the interaction between a bow and arrow are not difficult to derive, to calculate the energy and force involved, it is useful to consider the bow as a series of springs. When the bow is pulled back, there is energy stored in the outer regions of it akin to that of a spring being stretched. The archer exerts a compression force on the string-facing section of the wood while putting the outer sections under tension.
As we know, the potential energy stored in a spring is
where E is the elastic potential energy, k is the spring constant, and x is the extension of the spring. In theory, this would ideally all be converted to kinetic energy of the quantity
where v is the velocity of the arrow and m is its mass - and whilst we will continue to operate under this assumption for now, we must acknowledge that our estimates will be an approximation, due to the fact that we are ignoring resistive forces such as air resistance, and the sound energy and heat energy lost by the bow.
The force required for extension is
in accordance with Hooke’s law, where k is the spring constant of our bow and x is the displacement from its equilibrium position. Henceforth, the kinetic energy of an arrow being fired is directly proportional to the distance it is drawn back by the string attached to the bow. As a result, physically stronger bowmen could fire an arrow faster and further.
Practise your understanding of Hooke's Law below. "Softness" relates to the spring constant, k.
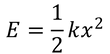
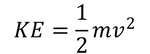
-
The optimum firing angle for maximum range of an arrow is 45⁰ from a horizontal, flat plane, as with a spear.
There is also physical analysis to be considered when looking at the damage caused by the arrow with regard to the arrow itself. Injuries sustained are related to the pressure exhibited by the arrow on the target. Pressure is given by the equation
where F is the force and A is the area of impact. Therefore arrowheads are heavy to maximise force, and sharp to minimise area, giving the greatest possible pressure and penetrative power to cause the maximum possible injury.




